一、什么是Sparse Kernel Machines
在kernel method那篇博客中,我们介绍了很多算法都可以用kernel来表示。但是其中有一个限制就是我们计算kernel matrix的时候必须对每一对Xn,Xm都计算一遍 ,其计算量是非常大的。所以有必要引入一种有着稀疏解的基于kernel的算法,在训练数据的子集上计算的kernel function即可,其对于新输入的预测仅仅依赖于稀疏kernel。而SVM就是Sparse Kernel Machines的一种。
SVM 是一种决策机,并不提供后验概率
二、什么是 SVM
假设我们有一个线性可分的数据集,我们可以使用很多线性算法来进行分类,但是往往其决策边界并不是最优的。比如感知机算法,虽然能够保证在有限步骤内找到一组解,但是其绘制的决策边界不仅依赖于初始参数值的选择,也依赖于数据集中数据被处理的顺序。而SVM算法引入了边缘(margin)这个概念来使得我们可以得到最优的决策边界,所谓边缘是指任一数据点到决策边界的最小距离。SVM的核心思想就是最大化margin,也被戏称为最大化“路的宽度”。
‘路’的两侧边沿到决策边界的距离相等,都等于margin,决策边界位于‘路’的中间

在上图的左、右两部分给出了两个不同的决策边界,但很明显左图的margin还并不是最大的,而右图给出了正确的决策边界。从图中我们可以看出,margin最大化的决策边界,其“路”的边沿一定通过了部分数据点,而在‘路’的中间没有任何数据点。
三、什么是支持向量
首先我们要理解所谓的向量是什么?
我们的数据集中的每一个数据点都处于一个特征空间当中,在这样的希尔伯特空间中,每一个点都可以用一个由空间原点指向该点的向量表示。因此支持向量机中的向量是指数据集中的数据点。
什么样的向量才能被称为支持向量?
在上图的右侧图中给出的决策边界,其margin被最大化了,我们可以看到,其“路”的边沿是通过了若干个数据点的。也就是说,‘路’的边沿仅仅由这若干个数据点就可以决定,这些能够确定决策边界的数据点被称为支持向量。
当我们预测新的输入时,只用这些数据点来确定决策边缘,然后判断新的输入位于决策边界的哪一侧即可。这样,我们就不用使用到所有的数据点,所以支持向量机是文章开头所提到的sparse kernel machine的一种
四、支持向量机的理论解释
1. 我们要考虑的简单模型
首先我们考虑这样一个二类分类问题,我们使用如下所示的线性模型:
不过我们也可以引入一个固定的特征空间映射,使得训练数据集在特征空间中是可分的,我们默认采用如下模型:
训练数据中有N个输入向量 ,对应的target value为 , 。
新的输入x根据y(x)的符号(正负)来分类。也就是说,在决策边界上,
对于训练数据中所有 的数据点, ,对于所有 的数据点, 。 这样可以得到:
但是这仅仅是一个很宽松的条件,仅仅考虑了决策边界。但是SVM的目标是使得margin最大化,同时决策边界到“路”的两侧边沿的距离是相等的,所以我们可以规定:
- 对于在’路’的边沿上的数据点
- 对于不在’路’的边沿上的数据点
- 对于训练数据中所有的点满足
这是我们要用到的第一个约束条件
2.如何计算’路’的宽度
SVM的思想就是最大化‘路’的宽度。那么’路’的宽度在我们的上述模型中如何定量得到呢?
在特征空间中,决策边界是与参数W相互垂直的

在上图中,假设有两个支持向量,分别用 , 表示,从 指向 的向量记作 ,还有一个与W同方向的单位向 ,那么’路‘的宽度等于在方向上的投影,即两者的内积:
这时由我们在上面提到的第一个约束条件我们知道, (注意这里为了表达的方便并没有使用特征映射函数)
所以我们得到了’路’的宽度为:
3.如何让‘路’的宽度最大化
我们已经得到了“路”的宽度的表达式,要想让路得宽度最大化,那么等价于让最小化,等价于让最小化。
同时我们还有一个约束条件,对于N个数据点,有:
利用拉格朗日乘数法,有
为拉格朗日乘数,。需要注意的是,,为了使得 最小化,我们在拉格朗日乘数部分前面加上的是负号。
根据拉格朗日乘数法,对W和b求导并令其导数为0,有:
将上式代回到中有:
上式需要满足如下两个条件:
至此我们已经将最小化的问题转变为了使得最大化的问题
因为在
中,要使得L最大,需要使得最大,而新的L(a)中当最大时,L(a)最大。所以我们把原来的最小化的问题转变为了使得最大化的问题
4.拉格朗日函数的对称表示
我们将’路的宽度’最大化问题转化成为了使得如下拉格朗日函数最大化的问题:
约束条件为:
对于,我们可以改写为:
所以原拉格朗日函数变为:
约束条件为:
5.二次规划问题的求解
那么如何找到能使得L(a)最大的呢?
这是一个二次规划问题(quardratic programming),属于数值优化的一种
在SVM中常见的有如下这三种方法:
-
QP 二次规划解法,可以保证找到最优解
-
SMO sequential minimal optimization 不一定每一次都能解出
-
LS least Squares
由于这一部分属于数值优化的部分,一般是使用他人优化的很好的代码即可,只要找到我们需要的
6. 如何求解 和b
在我们通过二次规划求解出来 之后,我们就可以通过 来计算得到 和b,从而得到决策边界
在上面3中,拉格朗日求导部分我们已经得到:
对于上面的最优化问题,我们可以得到如下的KKT条件:
对于训练数据中的每一个数据点,要么 ,要么 。
如果,那么该样本点就不会出现在下式中,:
只有 的时候才会出现在上式中,因此这些点才被称为支持向量。
利用这些支持向量,我们可以计算出b的值,考虑到 有:
又因,所以,那么将上式左右乘以有:
但是这里只使用了一个,我们可以使用所有的支持向量并求平均:
六、如何实现一个非线性的SVM
下面这段代码给出了一个非线性SVM的实例, 相关数据下载:
%matplotlib inline
import numpy as np
from scipy.linalg import norm
import cvxopt
import cvxopt.solvers
from pylab import *
data=np.loadtxt('data.txt')
# 获得训练数据
X = data[:,0:2]
t=data[:,2]
t = 2*t-3 # 将类别由1,2 转换成为-1,1
indexOfClass1=t==-1
indexOfClass2=t==1
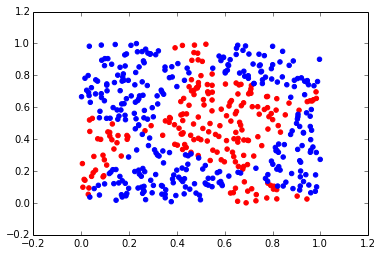
scatter(X[indexOfClass1,0],X[indexOfClass1,1],color='r')
scatter(X[indexOfClass2,0],X[indexOfClass2,1],color='b')
<matplotlib.collections.PathCollection at 0x10e802ad0>
"""
非线性SVM
使用了cvxopt中的Quadratic Programming,要先安装cvxopt:sudo -H pip install cvxopt
"""
N = len(X) #训练数据的个数
P = 3 # 多项式核的阶数
SIGMA = 0.125 # RBF kernel 中的sigma数,至于为什么将sigma设定为0.125就涉及到另外一个话题,参数寻找,可以查看我的其他博客
# 多项式 kernel
def polynomial_kernel(x, y):
return (1 + np.dot(x, y)) ** P
# RBF kernel
def gaussian_kernel(x, y):
return np.exp(- norm(x-y)**2 / (2 * (SIGMA ** 2)))
# 选定RBF kenel
kernel = gaussian_kernel
# 对于新的输入x求y(x)
def f(x, a, t, X, b):
summation = 0.0
for n in range(N):
summation += a[n] * t[n] * kernel(x, X[n])
return summation + b
# 计算gram matrix 注意这里根据 L(a)的公式部分将t_nt_jK(X_n,X_m)直接写在了一起
K = np.zeros((N, N))
for i in range(N):
for j in range(N):
K[i, j] = t[i] * t[j] * kernel(X[i], X[j])
#属于数值优化部分,不详解,请参考相关文档
Q = cvxopt.matrix(K)
p = cvxopt.matrix(-np.ones(N))
G = cvxopt.matrix(np.diag([-1.0] * N))
h = cvxopt.matrix(np.zeros(N))
A = cvxopt.matrix(t, (1, N))
b = cvxopt.matrix(0.0)
sol = cvxopt.solvers.qp(Q, p, G, h, A, b)
a = array(sol['x']).reshape(N)
# 找到支持向量,对于支持向量而言,a_n 不等于0
S = []
for n in range(len(a)):
if a[n] < 1e-5: continue
S.append(n)
# 计算b
summation = 0
for n in S:
temp = 0
for m in S:
temp += a[m] * t[m] * kernel(X[n], X[m])
summation += (t[n] - temp)
b = summation / len(S)
print S, b
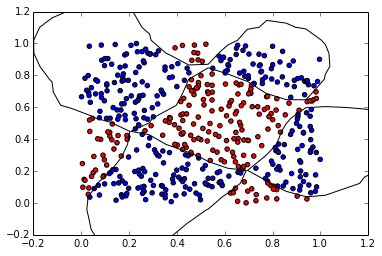
# 绘制训练数据
for n in range(N):
if t[n] > 0:
scatter(X[n,0], X[n,1], c='b', marker='o')
else:
scatter(X[n,0], X[n,1], c='r', marker='o')
# 绘制决策边界
X1, X2 = meshgrid(linspace(-2,2,50), linspace(-2,2,50))
w, h = X1.shape
X1.resize(X1.size)
X2.resize(X2.size)
Z = array([f(array([x1, x2]), a, t, X, b) for (x1, x2) in zip(X1, X2)])
X1.resize((w, h))
X2.resize((w, h))
Z.resize((w, h))
CS = contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower')
xlim(-0.2, 1.2)
ylim(-0.2, 1.2)
show()
pcost dcost gap pres dres
0: -1.1382e+02 -2.9664e+02 1e+03 3e+01 2e+00
1: -2.7149e+02 -4.4529e+02 7e+02 1e+01 1e+00
2: -4.5378e+02 -6.4589e+02 7e+02 1e+01 1e+00
3: -1.4698e+03 -1.7091e+03 8e+02 1e+01 9e-01
4: -1.7329e+03 -2.0083e+03 9e+02 1e+01 9e-01
5: -2.6332e+03 -3.0732e+03 1e+03 9e+00 7e-01
6: -3.3675e+03 -3.8939e+03 1e+03 5e+00 4e-01
7: -3.2772e+03 -3.5691e+03 5e+02 1e+00 1e-01
8: -3.3061e+03 -3.3833e+03 1e+02 3e-01 2e-02
9: -3.3118e+03 -3.3171e+03 6e+00 3e-03 2e-04
10: -3.3160e+03 -3.3161e+03 9e-02 2e-05 2e-06
11: -3.3160e+03 -3.3160e+03 2e-03 3e-07 2e-08
12: -3.3160e+03 -3.3160e+03 6e-05 3e-09 2e-10
Optimal solution found.
[33, 61, 62, 66, 90, 91, 93, 94, 95, 105, 121, 131, 138, 152, 160, 165, 172, 202, 206, 211, 215, 216, 233, 243, 249, 254, 334, 352, 366, 367, 370, 390, 407, 421, 423, 446, 456, 459, 461, 474, 489, 495, 497] -0.169196107517