Mixtures of Guassian

一、高斯分布与混合高斯

1.高斯分布的局限

虽然高斯分布有很多非常好的分析特性，但是当其对真实数据集进行建模的时候就会有很大的局限性。

比如美国黄石公园的old faithful 数据

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import multivariate_normal

s=np.loadtxt('old_faithful.txt')[:,1:]

#我们所需的数据在第一列和第二列，将其分别进行归一化
d_1_max=np.max(s[:,0])
d_1_min=np.min(s[:,0])
d_2_max=np.max(s[:,1])
d_2_min=np.min(s[:,1])
plt.scatter(s[:,0]/(d_1_max-d_1_min),s[:,1]/(d_2_max-d_2_min))

<matplotlib.collections.PathCollection at 0x10c364c10>

png

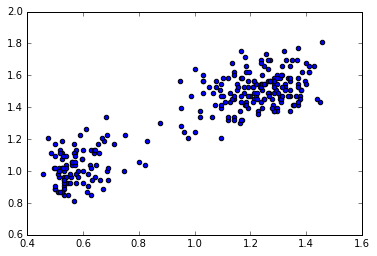
从上图可以看出，数据明显分成了两块，所以使用高斯分布是很难对这一数据集进行建模的。但是如果用两个高斯分布的线性重叠，则可以更好地描述上述数据集的特征。

2.混合高斯模型

选择适当数目的高斯分布，调整分布的均值和协方差，以及这些高斯分布的线性组合的系数，我们就能够以任意精度来近似描述任一个连续分布

我们将K个高斯分布的重叠表达如下：

$p(x)=\sum_{k=1}^K \pi_k N(x\vert \mu_k,\Sigma_k)$

上式被称作混合高斯，每个高斯分布 $N(x\vert \mu_k,\Sigma_k)$ 被称作混合分量，并且有着各自的均值和协方差

参数约束：
- $\pi_k$ ：混合系数（mixing coefficients）
如果我们对上面高斯混合公式进行积分，因为p(x)和右侧的高斯分布都是归一化的，所以有：

又由于要求 $p(x)\geq 0$ ,并且 $N(x\vert \mu_k,\Sigma_k) \geq 0$ ，所以每一个 $\pi_k \geq$ 。

因此：

3.混合高斯分布的图解

x=np.linspace(-0.5,1.5,100)
y=np.linspace(-0.5,1.5,100)

X, Y = np.meshgrid(x, y)
figure=plt.figure(figsize=(6,6))
plt.xlim(-0.5,1.5)
plt.ylim(-0.5,1.5)
plt.axis('equal')

pos = np.empty(X.shape + (2,))
pos[:, :, 0] = X; pos[:, :, 1] = Y
g1=multivariate_normal([0.2,0.4],[[1,0.8],[0.8,1]])
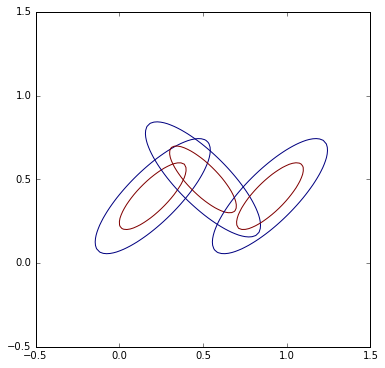
plt.contour(X, Y, g1.pdf(pos),[0.25,0.26])


g2=multivariate_normal([0.5,0.5],[[1,-0.8],[-0.8,1]])
plt.contour(X, Y, g2.pdf(pos),[0.25,0.26])

g3=multivariate_normal([0.9,0.4],[[1,0.8],[0.8,1]])
plt.contour(X, Y, g3.pdf(pos),[0.25,0.26])

<matplotlib.contour.QuadContourSet at 0x10fc50f10>

png

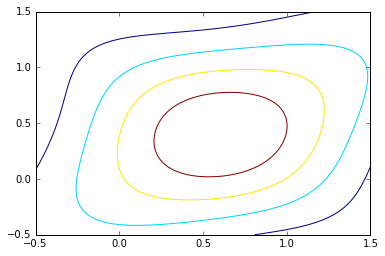
plt.contour(X,Y,0.3*g1.pdf(pos)+0.3*g2.pdf(pos)+0.4*g3.pdf(pos),5)

<matplotlib.contour.QuadContourSet at 0x110a71210>

png

4.高斯混合的贝叶斯视角

如果我们将 $\pi_k$ 视为第k个分量的先验概率，将密度 $N(x\vert \mu_k,\Sigma_k)$ 视为x关于k的条件概率，那么原高斯分布可以看成是x与k的联合分布的边缘分布。

$p(\mathbf{x})=\sum_{k=1}^{K}p(k)p(\mathbf{x} \vert k)$

而在第九章中我们将知道后验概率 $p(k \vert \mathbf{x})$ 起到了非常重要的作用，通常被称作responsibility。

$\gamma_k(\mathbf{x})=p(k \vert \mathbf{x})\\ =\frac{p(k)p(\mathbf{x} \vert k)}{\sum_l p(l)p(\mathbf{x} \vert l)}\\ =\frac{\pi_k N(x\vert \mu_k,\Sigma_k)}{\sum_l \pi_l N(x\vert \mu_l,\Sigma_l)}$

5.高斯混合的总结

高斯混合分布的决定参数有 $\mathbf{\pi} , \mathbf{\mu} ,\mathbf{\Sigma}$ ,其中：

$\mathbf{\pi}=\{\pi_1 ,\pi_2 ,...\pi_K\} \\ \mathbf{\mu} =\{\mu_1 ,\mu_2 ,...\mu_K \} \\ \mathbf{\Sigma} = \{\Sigma_1 ,...,\Sigma_K \}$

决定这些参数的一个方法最大似然，高斯混合分布的似然函数的对数为：

$lnp (\mathbf{X} \vert \pi ,\mu ,\Sigma )=\sum_{n=1}^{N}ln \left( \sum_{k=1}^{K} \pi_k N(x_n \vert \mu_k , \Sigma_k) \right)$

其中 $\mathbf{X} = \{\mathbf{x}_1,... \mathbf{x}_N \}$

我们可以看出，由于对数中的k个求和的存在，高斯混合比单个高斯分布要复杂得多。

而且这个式子的最大似然解法并没有闭式(closed-form)解，一种能使的似然函数最大化的解法是数值迭代法（梯度下降等）。不过在第九章，我们将会学习一种非常强大的框架——EM(expectation maximization)。