一、线性回归
参考PRML 3.1 与6.1
在这篇博客中,我们从最简单的线性回归模型出发,讨论基函数对原数据点的空间映射以及如何使得线性回归模型被扩展到非线性上,并且结合核化法给出线性回归模型的核化对偶表示。
1.什么是线性回归?
机器学习主要分为监督学习和非监督学习两大类别,其中监督学习是指训练数据既包含模型的输入数据,又包含模型对应的输出标签。根据模型输出是否是离散的,可以将监督学习分为分类和回归两大主题。
举一个简单的例子,对于垃圾邮件的识别就是一个分类问题,因为其输出的结果只有两种,垃圾邮件或者非垃圾邮件。但如果我们的问题是给定北京地区历年房价信息,我们要预测某一个房子的售价,这就是回归问题,因为这个房子的售价有无数个可能,但基本上跟房子的大小成正比。
回归的目标,简单来说就是给定一个n维度的输入,需要对m维度的输出进行预测,不过这个输出是连续变量。
最简单的回归是线性回归,即输出是输入变量的线性组合:
其中,模型的参数是,,因此上式可以改写为:
其中,一般被称为偏置(bias)。
二、线性基函数回归
1.什么是基函数
因为上述线性回归只能将模型表示成输入的线性组合,这样的模型有着非常多的约束,并无太大使用价值。我们必须要找到一种方法来使得我们的线性模型能够表示非线性,但又不失去其简单性。
因此我们引入了基函数的概念,所谓基函数就是特征映射,将原始输入数据映射到另一个空间当中,可以参考我的另一篇关于kernel method的博客,其中有非常详细的介绍。
我们用来表示基函数,比如这样一个简单的多项式映射:
 原始输入经过基函数映射后得到,
原来的线性模型为:
原始输入经过基函数映射后得到,
原来的线性模型为:
经过映射后:
在引入基函数之后,我们的模型任然是线性的,不过这个线性是针对映射后的数据而言,在此处是针对而言。
需要注意的是,基函数往往会改变原模型的参数的个数,比如原线性模型参数为3,映射后为4。
因此线性基函数回归可以表示为:
上式中,与的维度不一样,而与的维度一样。
在PRML一书中,这一节的符号标记有些许问题。不用考虑这种记号,最好只使用这一记号,即直接把整个原输入映射到另一个空间之中。
2.求解参数w
我们需要求得最佳的w,只需使平方和误差函数最小即可(sum-of-squares error function)。(在PRML中多次论述过,要使得在给定训练数据下输出为目标变量t的似然函数最大,对应于使得平方和误差函数最小)。
其中训练数据集中有n个数据点,输入数据为,目标变量为
为了推导方便,我们将原数据经过映射后表示为:
目标变量用表示,那么原误差函数可以表示为:
要使得误差函数最小,需要使其对于w的导数为0:
上述对参数 的求解被称为 normal equation
3.正则化
三、线性回归的核化表示
具体推导请看另一篇关于kernel method的博客
正则化的线性基函数表示中,我们推导出:
将w改写为:
将w重新代入到误差函数中:
令误差函数对的导数为0,我们可以得到:
将其代入到线性回归模型中,那么对于新的输入x有 其中的元素为。这是因为
因此线性回归模型完全可以用kernel function来表示
四、python实现
此处我们会看一个用线性回归来为一个sin函数建模,看一下不同的kernel function对拟合结果的影响
%pylab inline
class LinearModel(object):
"""
A generic linear regressor. Uses nonlinear basis functions, can fit with
either the normal equations or gradient descent
"""
def __init__(self, basisfunc=None):
"""
Instantiate a linear regressor. If you want to use a custom basis function,
specify it here. It should accept an array and output an array. The default
basis function is the identity function.
"""
self.w = array([])
self.basisfunc = basisfunc if basisfunc is not None else self.identity
def identity(self, x):
#identity basis function - for linear models in x
return x
def basismap(self, X):
#return X in the new basis (the design matrix)
Xn = zeros((X.shape[0], self.basisfunc(X[0,:]).shape[0]))
for i, xi in enumerate(X):
Xn[i,:] = self.basisfunc(xi)
return Xn
def fit_gd(self, X, y, itrs=100, learning_rate=0.1, regularization=0.1):
"""
fit using iterative gradient descent with least squares loss
itrs - iterations of gd
learning_rate - learning rate for updates
regularization - weight decay. Greated values -> more regularization
"""
#first get a new basis by using our basis func
Xn = self.basismap(X)
#initial weights
self.w = uniform(-0.1, 0.1, (Xn.shape[1],1))
#now optimize in this new space, using gradient descent
print 'initial loss:', self.loss(X,y)
for i in range(itrs):
grad = self.grad(Xn, y, regularization)
self.w = self.w - learning_rate*grad
print 'final loss:', self.loss(X,y)
def grad(self, X, y, reg):
"""
Returns the gradient of the loss function with respect to the weights.
Used in gradient descent training.
"""
return -mean((y - dot(X, self.w)) * X, axis=0).reshape(self.w.shape) + reg*self.w
def fit_normal_eqns(self, X, y, reg=1e-5):
"""
Solves for the weights using the normal equation.
"""
Xn = self.basismap(X)
#self.w = dot(pinv(Xn), y)
self.w = dot(dot(inv(eye(Xn.shape[1])*reg + dot(Xn.T, Xn)), Xn.T) , y)
def predict(self, X):
"""
Makes predictions on a matrix of (observations x features)
"""
Xn = self.basismap(X)
return dot(Xn, self.w)
def loss(self, X, y):
#assumes that X is the data matrix (not the design matrix)
yh = self.predict(X)
return mean((yh-y)**2)
Populating the interactive namespace from numpy and matplotlib
def fourier_basis(x):
#use sine waves with different amplitudes
sins = hstack(tuple(sin(pi*n*x)) for n in arange(0,1,0.1))
coss = hstack(tuple(cos(pi*n*x)) for n in arange(0,1,0.1))
return hstack((sins, coss))
def linear_basis(x): #includes a bias!
return hstack((1,x))
def polynomial_basis(x): #degree 10
return hstack(tuple(x**i for i in range(10)))
def sigmoid_basis(x): #offset sigmoids
return hstack(tuple((1+exp(-x-mu))**-1) for mu in arange(-9,9,0.5))
def heavyside_basis(x): #offset heavysides
return hstack(tuple(0.5*(sign(x-mu)+1)) for mu in arange(-9,9,0.5))
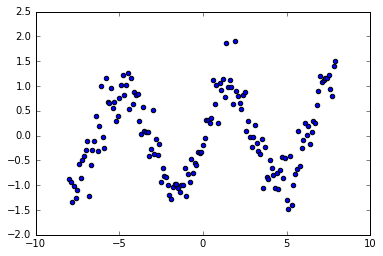
#generate some data
X = arange(-8, 8, 0.1).reshape((-1,1))
y = sin(X) + randn(X.shape[0],X.shape[1])*0.3
scatter(X, y)
<matplotlib.collections.PathCollection at 0x10f3af810>
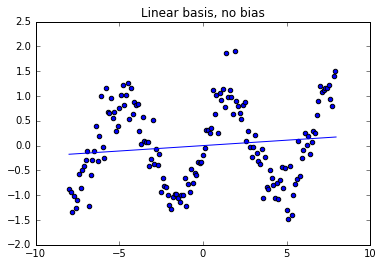
model = LinearModel()
model.fit_normal_eqns(X, y, reg=0.1)
Xn = arange(-8, 8, 0.05).reshape((-1,1))
yh = model.predict(Xn)
scatter(X, y)
plot(Xn, yh)
title('Linear basis, no bias')
show()
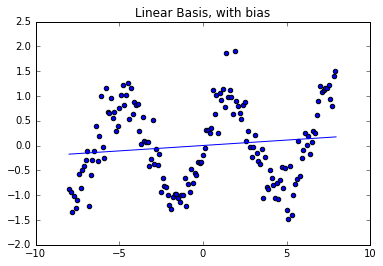
model = LinearModel(basisfunc=linear_basis)
model.fit_normal_eqns(X, y, 0.1)
Xn = arange(-8, 8, 0.05).reshape((-1,1))
yh = model.predict(Xn)
scatter(X, y)
plot(Xn, yh)
title('Linear Basis, with bias')
show()
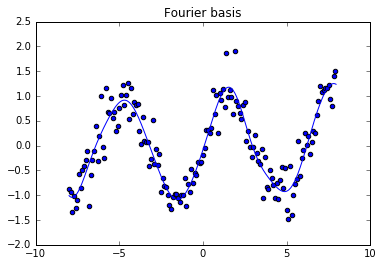
model = LinearModel(basisfunc=fourier_basis)
model.fit_normal_eqns(X, y, 0.1)
Xn = arange(-8, 8, 0.05).reshape((-1,1))
yh = model.predict(Xn)
scatter(X, y)
plot(Xn, yh)
title('Fourier basis')
show()
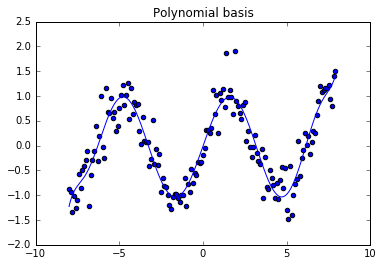
model = LinearModel(basisfunc=polynomial_basis)
model.fit_normal_eqns(X, y, 0.1)
Xn = arange(-8, 8, 0.05).reshape((-1,1))
yh = model.predict(Xn)
scatter(X, y)
plot(Xn, yh)
title('Polynomial basis')
show()
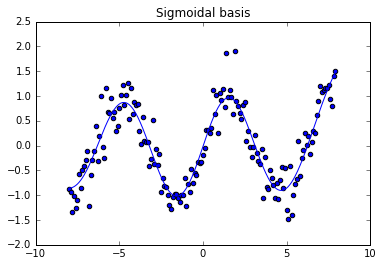
model = LinearModel(basisfunc=sigmoid_basis)
model.fit_normal_eqns(X, y, 0.1)
Xn = arange(-8, 8, 0.05).reshape((-1,1))
yh = model.predict(Xn)
scatter(X, y)
plot(Xn, yh)
title('Sigmoidal basis')
show()
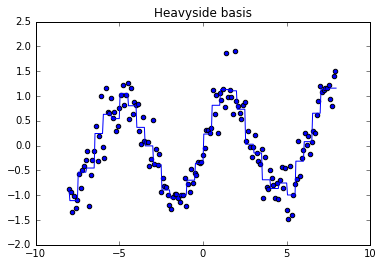
model = LinearModel(basisfunc=heavyside_basis)
model.fit_normal_eqns(X, y, 0.1)
Xn = arange(-8, 8, 0.05).reshape((-1,1))
yh = model.predict(Xn)
scatter(X, y)
plot(Xn, yh)
title('Heavyside basis')
show()