Auto selection of RBF kernel parameter

RBF kernel

一、数学表达式与一些简单的性质

RBF kennel 又被称为高斯kernel，其数学表达式为:

$k(x,z)=\exp(-\frac{\begin{Vmatrix}x-z \end{Vmatrix} ^2}{2\sigma^2})$

通过数学表达式我们可以发现，任何一个原空间中的数据点被映射到特征空间之中，其到特征空间原点的距离的平方为：

$norm^2=\phi(x)^T\phi(x)=k(x,x)=\exp(-\frac{\begin{Vmatrix}x-x \end{Vmatrix} ^2}{2\sigma^2})=1$

另外，任意两个数据点在特征空间中的相似可以用其向量(由特征空间的原点指向数据点)的夹角余弦表示：

$\cos (\theta)=\frac{\phi(x_1)^T \phi(x_2)}{\begin{Vmatrix}\phi(x_1)\end{Vmatrix}\begin{Vmatrix}\phi(x_2)\end{Vmatrix}}=\phi(x_1)^T \phi(x_2)=k(x_1,x_2)$

所以任意两点之间的余弦就等于kernel 函数的数值

所以RBF kernel的性质非常得优雅：

在特征空间中，每一个数据点的norm都为1且为正所以每一个数据点都被映射到特征空间的超球面的表面上任意两点之间的相似程度由向量的余弦表示，也就是两点的kernel 函数值表示

如下图所示:

二、数据点相似程度的直观解释

如果两个数据点的余弦距离接近1，那么这两个点在特征空间中非常相似
如果这两个数据点的余弦距离越接近0，那么这两个点在特征空间中越不相似

我们使用kernel的目的就是要使得原来非线性可分的点在特征空间中可分，那么我们使用RBFkernel的目的也是尽量使得数据点在特征空间中更容易线性可分。

因此我们的目标是使得相同类别的点的向量方向尽可能相同，即余弦接近1，而不同类别的点尽量方向接近九十度，余弦接近0.

那么对于RBF kernel来说，只有一个参数 $\sigma$ 控制着这些数据点在特征空间中相似程度。

$k(x,z)=\exp(-\frac{\begin{Vmatrix}x-z \end{Vmatrix} ^2}{2\sigma^2})$

当 $\sigma$ 非常小的时候，k(x,z)=0,任意两点之间角度为90度，不相似
当 $\sigma$ 非常大的时候，k(x,z)=1,任意两点之间角度为0度，向量重合在一起，非常相似

那么随着 $\sigma$ 从小到大变化的时候，原来更相近的两个点向量夹角减小地越快，而原来不相近的点向量夹角减少地越慢，因此当 $\sigma$ 取某个值的时候，同一个类别的点和不同类别的点被分开，并且效果最好

我们用 $w(\sigma)$ 表示同一类别中的数据点之间的余弦值的平均

我们用 $b(\sigma)$ 表示不同类别中的数据点之间的余弦值的平均

我们的目标是要找到一个 $\sigma$ ，使得

$w(\sigma) \rightarrow 1^- \\ b(\sigma) \rightarrow 0^+$

也就是说要要到一个 $\sigma$ ，使得：

$1-w(\sigma) \rightarrow 0^+ \\ b(\sigma) \rightarrow 0^+$

因此决策函数被定义为：

$J(\sigma)=(1-w(\sigma))+b(\sigma)=1-w(\sigma)+b(\sigma)$

Python 实现

我们的目标是求出 $w(\sigma) \text{ and } b(\sigma)$ ,

我们如果能够从kernel matrix中找到所有属于同一个类别的点，将其RBF kernel 函数值相加起来就可以得到所有属于同一个类别的kernel值

再将整个kernel matrix中的值相加减掉刚才属于同一个类别的kernel 值，就是属于不同类别的kernel值之和

再将两者除以各自的数量，就可以得到平均值

假设有三个不同的类别，如下图所示：

上图只是为了表示方便，我们计算矩阵K的时候不用按照类别的顺序

把上图中的阴影部分加起来除以相应的个数就是w，把整个矩阵减掉阴影部分加起来再除以相应的个数就是b

%matplotlib inline

from sklearn.svm import SVC
import numpy as np
from matplotlib import pyplot as plt
from sklearn import datasets

# 获得训练数据
iris = datasets.load_iris()

X=iris.data
t=iris.target

from scipy.linalg import norm
from sklearn.metrics.pairwise import rbf_kernel

SIGMA=0.5
def cal_J(gamma):
    
    X=iris.data
    t=iris.target
    K=rbf_kernel(X,gamma=gamma)
    numberOfClass=len(np.unique(t))

    #计算同类别的kernel 值得总和
    sameClassSum=0

    #为了计算w我们需要统计每一个类别的数据点的个数
    numberOfClassSample=[]
    block1=K[0:51,0:51]
    for label in np.unique(t):
        IndexOfThisLabel=t==label
        sameClassSum+=np.sum(K[np.ix_(IndexOfThisLabel,IndexOfThisLabel)])
        numberOfClassSample.append(np.sum(IndexOfThisLabel))

    #print numberOfClassSample
    diffClassSum=np.sum(K)-sameClassSum

    w=sameClassSum/np.sum(np.square(numberOfClassSample))

    b=diffClassSum/(np.square(np.sum(numberOfClassSample))-np.sum(np.square(numberOfClassSample)))

    J=1-w+b
    return J

sigmaValue=np.arange(0,2,0.02)
J=np.zeros_like(sigmaValue)
for i in xrange(len(sigmaValue)):
    J[i]=cal_J(sigmaValue[i])
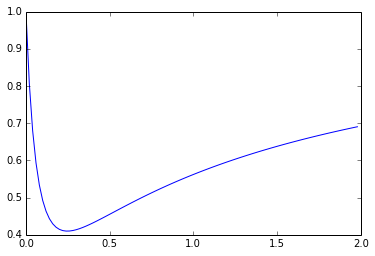
plt.plot(sigmaValue,J)

[<matplotlib.lines.Line2D at 0x115b0d4d0>]

png

from scipy.optimize import minimize

minimize(cal_J,0.2)

   status: 0
  success: True
     njev: 6
     nfev: 18
 hess_inv: array([[ 0.30520045]])
      fun: 0.40991833280965956
        x: array([ 0.24713584])
  message: 'Optimization terminated successfully.'
      jac: array([  4.19095159e-06])

结合图示和scipy的最优化函数可以看出来，当gamma等于0.24713584的时候，J最小，为0.40991833280965956