%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
from pylab import *
概率生成模型
首先考虑二分类情况,类别C1 的后验概率可以写成:
其中,
是logistic sigmoid函数,定义为
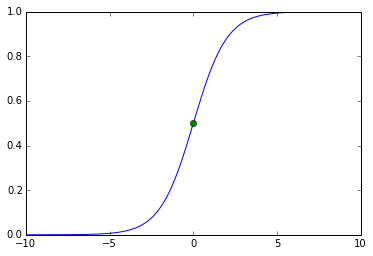
sigmoid函数图形为s形,其满足下面这几个性质:
其反函数为
,它表示两个类别的概率比值的对数:
我们从simoid函数的定义可以看出,
所以有
def sigmoid(x):
return 1/(1+np.exp(-x))
x=np.arange(-10,10,0.01)
y=sigmoid(x)
plt.plot(x,y)
plt.plot(0,0.5,'go')
plt.show()
多分类情况
其中$$a_k=lnp(x\vert C_k)p(C_k)$$
上述函数被称为归一化指数(normalized exponential),也被称为softmax函数,因为它表示“max”函数的一个平滑版本。这是因为,如果对于所有的 $$j\neq ka_k » a_jp(C_k\vert x)≃1p(Cj\vert x)≃0$$。
N=100
def f(x1, w):
# 决策边界的直线方程
# p(C1\vert X) > 0.5 -> X属于类别C1
# p(C1\vert X) < 0.5 -> X属于类别C2
# p(C1\vert X) = 0.5 -> sigmoid函数的输入为0
a = - (w[1] / w[2])
b = - (w[0] / w[2])
return a * x1 + b
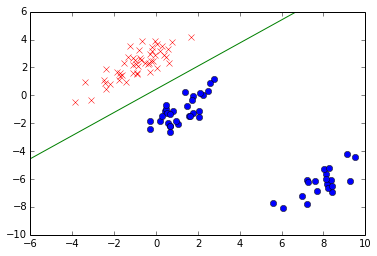
# 生成训练数据
cls1 = []
cls2 = []
mean1 = [-1, 2]
mean2 = [1, -1]
mean3 = [8, -6]
cov = [[1.0,0.8], [0.8,1.0]]
# 假设数据服从多维高斯分布
cls1.extend(np.random.multivariate_normal(mean1, cov, N / 2))
cls2.extend(np.random.multivariate_normal(mean2, cov, N / 2 - 20))
cls2.extend(np.random.multivariate_normal(mean3, cov, 20))
# 创建输入矩阵X
temp = vstack((cls1, cls2))
temp2 = ones((N, 1))
X = hstack((temp2, temp))
# 创建target矩阵T(注意这里不是1-of-K的表示方法)
t = []
for i in range(N / 2):
t.append(1.0)
for i in range(N / 2):
t.append(0.0)
t = array(t)
# 用IRLS方法更新参数w
turn = 0
w = array([0.0, 0.0, 0.0]) # 为参数w设定适当的初始值
while True:
# 计算 phi 由于没有使用固定的基函数,phi恒等于输入矩阵X
phi = X
# 计算R和Y
R = np.zeros((N, N))
y = []
for n in range(N):
# a=W^T\phi
a = np.dot(w, phi[n,])
y_n = sigmoid(a)
# R 是一个对角矩阵
R[n, n] = y_n * (1 - y_n)
y.append(y_n)
# 计算海森(Hessian)矩阵H
phi_T = phi.T
H = np.dot(phi_T, np.dot(R, phi))
# 更新参数W
w_new = w - np.dot(np.linalg.inv(H), np.dot(phi_T, y-t))
# 判断w是否收敛
#np.linalg.norm 用于计算向量的2-范数
diff = np.linalg.norm(w_new - w) / np.linalg.norm(w)
if diff < 0.1: break
w = w_new
turn += 1
# 绘制训练数据点
x1, x2 = np.array(cls1).transpose()
plot(x1, x2, 'rx')
x1, x2 = np.array(cls2).transpose()
plot(x1, x2, 'bo')
# 绘制训练边界
x1 = np.linspace(-6, 10, 1000)
x2 = [f(x, w) for x in x1]
plot(x1, x2, 'g-')
xlim(-6, 10)
ylim(-10, 6)
show()
/Library/Python/2.7/site-packages/ipykernel/__main__.py:66: RuntimeWarning: divide by zero encountered in double_scalars
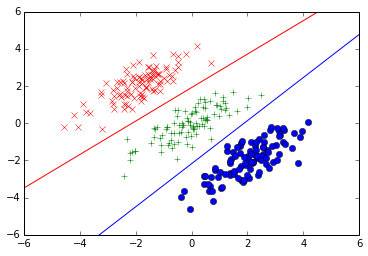
# 4.3.4 多类别逻辑回归
N = 300 # 数据的数目
M = 3 # 参数的维度
K = 3 # 类别的数目
def sigmoid(a):
return 1 / (1 + np.exp(-a))
def f(x1, W_t, c1, c2):
# 类别C1和类别C2的决策边界的直线方程
a = - ((W_t[c1, 1] - W_t[c2, 1]) / (W_t[c1, 2] - W_t[c2, 2]))
b = - ((W_t[c1, 0] - W_t[c2, 0]) / (W_t[c1, 2] - W_t[c2, 2]))
return a * x1 + b
# 生成训练数据
cls1 = []
cls2 = []
cls3 = []
mean1 = [-2, 2] # 类别1的均值
mean2 = [0, 0] # 类别2的均值
mean3 = [2, -2] # 类别3的均值
cov = [[1.0,0.8], [0.8,1.0]] # 公用协方差矩阵
# 假定训练数据满足多维高斯分布
cls1.extend(np.random.multivariate_normal(mean1, cov, N / 3))
cls2.extend(np.random.multivariate_normal(mean2, cov, N / 3))
cls3.extend(np.random.multivariate_normal(mean3, cov, N / 3))
# 生成输入矩阵X
temp = vstack((cls1, cls2, cls3))
temp2 = ones((N, 1))
X = hstack((temp2, temp))
# 生成target 矩阵T (采用1-of-K的表示方法)
T = []
for i in range(N / 3):
T.append(array([1, 0, 0]))
for i in range(N / 3):
T.append(array([0, 1, 0]))
for i in range(N / 3):
T.append(array([0, 0, 1]))
T = array(T)
# 利用IRLS算法更新参数矩阵W
turn = 0
W = np.zeros((M, K))
while True:
# 由于没有使用固定基函数,phi恒等于X
phi = X
# 计算预测矩阵Y
Y = np.zeros((N, K))
for n in range(N):
denominator = 0.0
for k in range(K):
denominator += np.exp(np.dot(W[:,k], X[n,:]))
for k in range(K):
Y[n, k] = np.exp(np.dot(W[:,k], X[n,:])) / denominator
# 计算海森矩阵H
I = np.identity(K)
H = np.zeros((K * K, M, M))
for j in range(K):
for k in range(K):
# 按照4.110式子来计算
for n in range(N):
temp = Y[n, k] * (I[k, j] - Y[n,j])
H[k + j * K] += temp * matrix(phi)[n].reshape(M,1) * matrix(phi)[n].reshape(1,M) #
# 也可以按照如下矩阵来进行计算
#Ijk = 1 if j == k else 0
#R = np.diag(Y[:,k] * (Ijk - Y[:,j]))
#H[k + j * K] = np.dot(phi.T, np.dot(R, phi))
# 更新权重矩阵W
W_new = np.zeros((M, K))
phi_T = phi.T
for i in range(K):
temp = np.dot(phi_T, Y[:,i] - T[:,i])
W_new[:,i] = W[:,i] - np.dot(np.linalg.inv(H[i + i * K]), temp)
# 判断W是否收敛
diff = np.linalg.norm(W_new - W) / np.linalg.norm(W)
if diff < 0.1: break
W = W_new
turn += 1
W_t = np.transpose(W)
# 绘制训练数据点
x1, x2 = np.transpose(np.array(cls1))
plot(x1, x2, 'rx')
x1, x2 = np.transpose(np.array(cls2))
plot(x1, x2, 'g+')
x1, x2 = np.transpose(np.array(cls3))
plot(x1, x2, 'bo')
# 绘制类别C1和类别C2的决策边界
x1 = np.linspace(-6, 6, 1000)
x2 = [f(x, W_t, 0, 1) for x in x1]
plot(x1, x2, 'r-')
# 绘制类别C2和类别C3的决策边界
x1 = np.linspace(-6, 6, 1000)
x2 = [f(x, W_t, 1, 2) for x in x1]
plot(x1, x2, 'b-')
xlim(-6, 6)
ylim(-6, 6)
show()
/Library/Python/2.7/site-packages/ipykernel/__main__.py:84: RuntimeWarning: divide by zero encountered in double_scalars
====