Multivariate normal distribution

多变量正态分布

单变量正态分布的分布函数为：

$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp{\left( - \frac{(x-\mu)^2}{2\sigma^2} \right)}$

多变量正态分布的分布函数为：

$f(x)=\frac{1}{(2\pi)^{2/d}\vert \Sigma \vert^{1/2}}\exp \left( -\frac{1}{2}(x-\bar{x})^T \Sigma^{-1} (x-\bar{x})\right)$

相比单变量正态分布，多变量正态分布中的均值和方差有所不同

每一个变量都有相应的均值，多个变量的均值组成了相应的均值向量方差用协方差矩阵表示，协方差矩阵对角线上元素表示每个变量的分布情况，其他元素表示元素之间的分布情况

首先我们要了解多变量正态分布的基本几何含义/均值向量与协方差矩阵

1.Euclidean Distance

欧氏距离表示为： $\begin{Vmatrix}x-\bar{x}\end{Vmatrix}_{\Sigma}^2=(x-\bar{x})^T (x-\bar{x})=k^2$

如上图所示，空间中其他点到一定点的欧氏距离可以表示为以该定点为中心的同心圆

2.Mahalanobis Distance

$\begin{Vmatrix}x-\bar{x}\end{Vmatrix}_{\Sigma}^2=(x-\bar{x})^T \Sigma^{-1}(x-\bar{x})=k^2$

covariance matrix $\Sigma=\frac{1}{n}\sum_{i=1}^{N}(x_i-\bar{x})(x_i-\bar{x})^T$

在数学中， $\Sigma$ 为正半定或者正定矩阵即可，我们可以认为欧氏距离是马氏距离的特例，欧氏距离中的 $\Sigma$ 为单位矩阵

2.1 对角化

对角化定理

如果A是一个d×d的实对成矩阵(real symmetric)，那么一定存在一个正交矩阵P使得 $P^TAP=D$ ,其中D是对角矩阵且其对角线上的元素为A的特征值

证明 $\Sigma$ 是一个对称矩阵

$\Sigma ^T=\left\{ \frac{1}{n}\sum_{i=1}^{N}(x_i-\bar{x})(x_i-\bar{x})^T \right\}^T \\ =\frac{1}{n}\sum_{i=1}^{N}\left\{ (x_i-\bar{x})(x_i-\bar{x})^T \right\}^T \\ =\frac{1}{n}\sum_{i=1}^{N} \left\{ (x_i-\bar{x}) ^T\right\}^T (x_i-\bar{x})^T \\ =\frac{1}{n}\sum_{i=1}^{N}(x_i-\bar{x})(x_i-\bar{x})^T \\ =\Sigma$

$\Sigma$ 的分解

设 $\Sigma$ 可以分解为 $\Sigma=VDV^T$ ,其中V为 $\Sigma$ 的特征向量组成的矩阵，D为 $\Sigma$ 的特征值组成的对角矩阵

$V=[e_1,e_2,....e_d]\\ D=diag\{\lambda_1,....,\lambda_d\}\\ =\begin{bmatrix}\frac{1}{\lambda_1}&\cdots&0\\\vdots &\ddots&\vdots\\0&\cdots&\frac{1}{\lambda_d}\end{bmatrix}$

那么 $\Sigma 的逆为$ $\Sigma^{-1}=\left( VDV^T\right)^{-1}=(V^T)^{-1}D^{-1}V^{-1}\\ =\left( VDV^T\right)^{-1}\\ =(V^T)^{-1}D^{-1}V^{-1}\\ =(V^{-1})^{-1}D^{-1}V^T\\ =VD^{-1}V^T\\ =[e_1,e_2,....e_d] \begin{bmatrix}\frac{1}{\lambda_1}&\cdots&0\\\vdots &\ddots&\vdots\\0&\cdots&\frac{1}{\lambda_d}\end{bmatrix} \begin{bmatrix}e_1^T\\\vdots\\e_d^T \end{bmatrix}\\ =\left[ \frac{e_1}{\lambda_1},...\frac{e_d}{\lambda_d}\right] \begin{bmatrix}e_1^T\\\vdots\\e_d^T \end{bmatrix}\\ =\frac{1}{\lambda_1}e_1e_1^T+\frac{1}{\lambda_2}e_2e_2^T+....+\frac{1}{\lambda_d}e_de_d^T$

2.2马氏距离的几何含义

$\begin{Vmatrix}x-\bar{x}\end{Vmatrix}_{\Sigma}^2 =\\ (x-\bar{x})^T \Sigma^{-1}(x-\bar{x}) \\ =(x-\bar{x})^T \left(\frac{1}{\lambda_1}e_1e_1^T+ \frac{1}{\lambda_2}e_2e_2^T \right)(x-\bar{x}) \\ =\frac{1}{\lambda_1}(x-\bar{x})^T e_1e_1^T(x-\bar{x}) + \frac{1}{\lambda_2}(x-\bar{x})^T e_2e_2^T(x-\bar{x}) \\ =\frac{y_1^2}{(\sqrt{\lambda_1})^2} + \frac{y_2^2}{(\sqrt{\lambda_2})^2}$

其中：

$(x-\bar{x})^T e_1e_1^T(x-\bar{x})\\ =\left\{ (x-\bar{x})^T e_1 \right\} \left\{ e_1^T(x-\bar{x}) \right\} \\ =\left\{ e_1^T(x-\bar{x}) \right\}^T \left\{ e_1^T(x-\bar{x}) \right\} \\ =y_1^2$

$e_1^T(x-\bar{x})$ 表示 $(x-\bar{x})$ 这个向量在 $e_1$ 上的投影向量，用 $y_1$ 表示，如下图所示：

因此，马氏距离可以看成是以定点为中心的椭圆

3. 多变量正态分布的推导

多变量正态分布的分布函数可以认为是由多个相应的单变量的分布函数相乘得到的：

4.python 演示

4.1 实对称矩阵的分解

import numpy as np
A=np.array([[0,2,2],[2,0,2],[2,2,0]],dtype=np.float64)
A

array([[ 0.,  2.,  2.],
       [ 2.,  0.,  2.],
       [ 2.,  2.,  0.]])

#利用numpy可以很简单地算出A的特征值和特征向量
D,P=np.linalg.eigh(A)

D #D为A的特征值

array([-2., -2.,  4.])

P #P 是A的特征向量，是一个正交矩阵

array([[ 0.69868277,  0.42250331, -0.57735027],
       [ 0.01655721, -0.81632869, -0.57735027],
       [-0.71523999,  0.39382538, -0.57735027]])

np.dot(P,P.T)  #可见P与P.T 的乘积是一个单位矩阵

array([[  1.00000000e+00,   0.00000000e+00,   2.77555756e-16],
       [  0.00000000e+00,   1.00000000e+00,  -1.66533454e-16],
       [  2.77555756e-16,  -1.66533454e-16,   1.00000000e+00]])

4.2 多变量高斯分布的3D展示

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import multivariate_normal
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter

#产生一个从二维的从-3到3的meshgrid
x1=np.arange(-3,3,0.2)

x2=np.arange(-3,3,0.2)

X1,X2=np.meshgrid(x1,x2)


#X_combine是将X1,X2合并成为一个新的矩阵，矩阵的每一个元素是由X1和X2的相同位置的元素组成的一个2维矩阵，这个2维矩阵就是我们计算
#多变量高斯分布的输入(在我们的实例中是一个2变量)
#下面的这种合并方式具有一般性，应该记住
X_combine=np.vstack(([X1.T], [X2.T])).T


#计算每一个点的相应多变量高斯分布的概率值
c=multivariate_normal.pdf(X_combine,[1,1],[[0.5,0.4],[0.4,0.5]])



#绘制图形
fig = plt.figure()
ax = fig.gca(projection='3d')

surf = ax.plot_surface(X1, X2, c, rstride=1, cstride=1, cmap=cm.coolwarm,
                       linewidth=0, antialiased=False)
ax.set_zlim(0, 1.01)

ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))

fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()

#如果去掉 %matplotlib inline 可以打开一个图形窗口，在这个窗口里可以放大和旋转这个3D图形

png

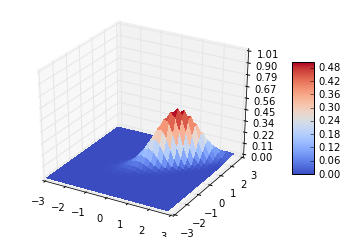
4.3 产生多变量正态分布的数据

我们在机器学习中经常假设数据满足多变量正态分布，因此我们需要能够产生需要的数据

#确定两个不同的2变量高斯分布的均值向量和协方差矩阵
mean1 = [-1, 2]
mean2 = [4, -6]
cov1 = [[1.0,0.8], [0.8,1.0]]
cov2=  [[0.5,0.2],[0.2,0.5]]

#为每一种分布产生150个数据
data1=np.random.multivariate_normal(mean1,cov1,150)
data2=np.random.multivariate_normal(mean2,cov2,150)

fig=plt.figure()
plt.plot(data1[:,0],data1[:,1],'rx')
plt.plot(data2[:,0],data2[:,1],'bo')

plt.xlim(-6, 10)
plt.ylim(-10, 6)
plt.show()

png

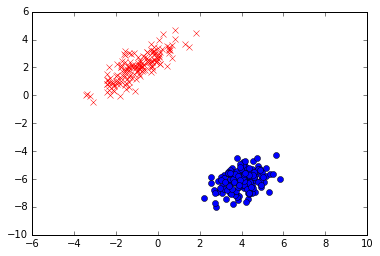
从上图可以看出，多变量高斯分布的数据多集中在均值向量处，协方差矩阵印象数据点的倾斜程度和离散程度