k-means cluster

一、聚类

聚类是无监督学习的一种，我们的数据集只有原始观察数据，而不像在监督学习中每一个数据点还有对应的target label。我们的目标就是将这些数据点进行聚类，根据数据的分布将数据分配到多个类别中去。

假定我们有N个D-维欧式变量 $\mathbf{x}$ 组成的数据集 ${\mathbf{x}_1,,,,\mathbf{x}_N}$ ,
我们的目标是把数据集分成K个簇（我们可以认为K是预先给定的）。
直观上讲,我们会认为由一组数据点构成的一个聚类中,聚类内部点之间的距离应该小于数据点与聚类外部的点之间的距离。
我们可以形式化地说明这个概念。引入一组D维向量μk,其中k = 1, . . . , K,且μk是与第k个聚类关相联。我们可以认为μk代表第k个簇的中心点。
我们的目标是找到向量集合{μk}，并且将数据点分配到k个簇中去，并且使得每个数据点到其最近的向量μk之间的距离的平方和最小。

1. 目标函数的确定

为了方便我们的描述，我们可以先定义好一些记号来描述数据点和簇之间的分配关系。对于每一个数据点 $\mathbf{x}_n$ ,我们引入了对应的二项指示器变量集合 $r_{nk} \in \{0,1\},k=1,....,K$ 。如果数据点 $\mathbf{x}_n$ 被分配到第k个簇中去，那么 $r_{nk}=1$ 并且 $r_{nj}=0,j \neq k$ 。因此我们可以定义目标函数（objective function），有时候被称为失真函数(distortion measure)为：

$\mathbf{J}=\sum_{n=1}^N \sum_{k=1}^K r_{nk} \vert \mathbf{x}_n - \mu _k\vert^2$

从上面的定义可以看出，目标函数被定义为每一个数据点到它所在簇的中心点的距离的平方和。我们的目标是找到合适的 $\{r_{nk}\}$ 以及 $\{\mu _k\}$ 使得目标函数最小。

2.最小化目标函数

目标函数与两个参数有关， $r_{nk}$ 以及 $\mu_k$ 。我们可以利用两步迭代过程来优化目标函数，在第一步中对 $r_{nk}$ 进行优化，在第二步中对 $\mu_k$ 进行优化。

首先我们为 $\mu_k$ 设定初始值。

在第一步中保持 $\mu_k$ 不变，找出使得J最小的 $r_{nk}$

在第二步中保持 $r_{nk}$ 不变，找出使得J最小化的 $\mu_k$ 。

重复以上两步优化过程直至收敛

3. 关于 $r_{nk}$ 对J进行优化

$\mathbf{J}=\sum_{n=1}^N \sum_{k=1}^K r_{nk} \vert \mathbf{x}_n - \mu _k\vert^2$

因为每一个数据点的 $r_{nk}$ 是相互独立的，因此对于不同的n我们可以选择我们选择使得 $\vert \mathbf{x}_n - \mu _k\vert^2$ 最小的的k值并且使得 $r_{nk}=1,r_{nj}=0,j \neq k$ 。简单来说，这一步就是将第n个数据点分配给离它最近的簇的中心点。

更一般化来说，上述过程可以表述为：

$r_{nk} = \begin{cases} 1 & \quad \text{if } k=arg min_j \vert \mathbf{x}_n - \mu _k\vert^2\\ 0 & \quad \text{otherwise}\\ \end{cases}$

4.关于 $\mu_k$ 对J进行优化

保持 $r_{nk}$ 不变对 $\mu_k$ 进行优化。目标函数是 $\mu_k$ 的二次函数，我们可以令目标函数对 $\mu_k$ 的求导为0，从而得到：

$2\sum_{n=1}^N r_{nk}(\mathbf{x}_n-\mu_k)=0\\ \Rightarrow\\ \mu_k=\frac{\sum_n r_{nk} \mathbf{x}_n}{\sum_nr_{nk}}$

从上式可以看出， $\mu_k$ 等于所有分配到簇k的数据点的均值。

5.对于k-means算法过程的总结

任意选择k个中心点
将每个点分配到离其最近的簇中 3.将第k个簇的中心点设为该簇中所有数据点的均值 4.如果不收敛，重复2、3、4

6.k-means算法的收敛问题

因为迭代过程中的每一步都在减少J值，所以该算法一定可以收敛。但是有可能改算法只是找到J局部最优解而非全局最优解。

7. python 实现

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt

在这里我们使用美国黄石公园的old faithful 数据

s=np.loadtxt('old_faithful.txt')[:,1:]

#我们所需的数据在第一列和第二列，将其分别进行归一化
d_1_max=np.max(s[:,0])
d_1_min=np.min(s[:,0])
d_2_max=np.max(s[:,1])
d_2_min=np.min(s[:,1])
plt.scatter(s[:,0]/(d_1_max-d_1_min),s[:,1]/(d_2_max-d_2_min))

<matplotlib.collections.PathCollection at 0x109ab8cd0>

png

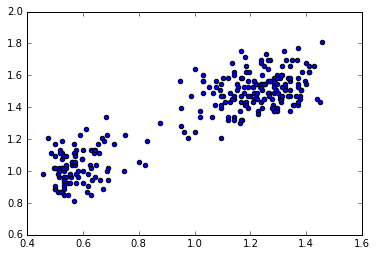
fig=plt.figure()

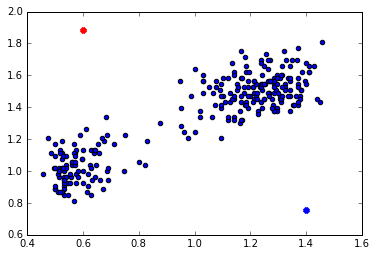
# 我们假定k-means算法的初始簇为两个，对这两个簇任意选择中心点
mu_1=np.array([2.1,100])
mu_2=np.array([4.9,40])
plt.scatter(s[:,0]/(d_1_max-d_1_min),s[:,1]/(d_2_max-d_2_min))
plt.scatter(mu_1[0,np.newaxis]/(d_1_max-d_1_min),mu_1[1,np.newaxis]/(d_2_max-d_2_min),c='r',marker='x',linewidths=4)
plt.scatter(mu_2[0,np.newaxis]/(d_1_max-d_1_min),mu_2[1,np.newaxis]/(d_2_max-d_2_min),c='b',marker='x',linewidths=4)
plt.show()

png

# 为每一个点分配簇

#distance1 为各点到簇1 的距离平方值
distance1=np.sum(np.square(s-mu_1),axis=1)
distance2=np.sum(np.square(s-mu_2),axis=1)

distance=np.hstack((distance1.reshape(len(distance1),1),distance2.reshape(len(distance1),1)))

clsuterOfEachDataPoint=np.argmin(distance,axis=1)

#将属于某个簇的所有数据点的均值作为新的簇的中心点

dataPointOfCluster1=s[clsuterOfEachDataPoint==0]
dataPointOfCluster2=s[clsuterOfEachDataPoint==1]

mu_1=np.mean(dataPointOfCluster1,axis=0)
mu_2=np.mean(dataPointOfCluster2,axis=0)

figure=plt.figure()
plt.scatter(s[:,0]/(d_1_max-d_1_min),s[:,1]/(d_2_max-d_2_min))
plt.scatter(mu_1[0,np.newaxis]/(d_1_max-d_1_min),mu_1[1,np.newaxis]/(d_2_max-d_2_min),c='r',marker='x',linewidths=6)
plt.scatter(mu_2[0,np.newaxis]/(d_1_max-d_1_min),mu_2[1,np.newaxis]/(d_2_max-d_2_min),c='b',marker='x',linewidths=6)
plt.show()

png

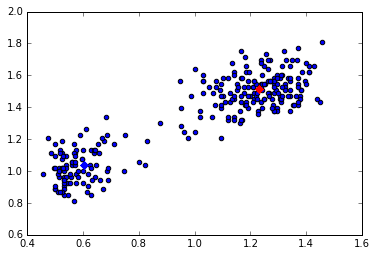
经过上面第一次迭代，中心点的位置基本处于两个簇的中心了，重复此过程，就能得到一个收敛解